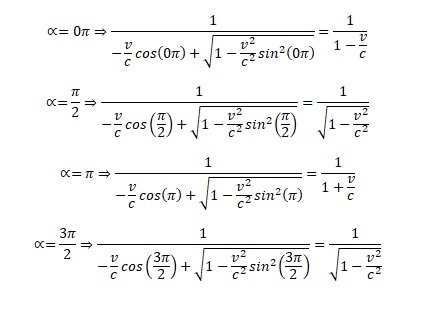Another solutions

To begin with, we will revive the standard calculation of the Lorentz transformation

https://archive.org/download/BeiserConceptsOfModernPhysicsText/Beiser-ConceptsOfModernPhysics_text.pdf

Arthur Beiser - Concepts of Modern Physics

THE LORENTZ TRANSFORMATION

A reasonable guess as to the nature of the correct relationship between x and x' is 

1.18

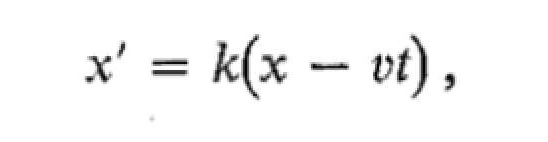
where k is a factor of proportionality that does not depend upon either x or t but may be a function of v. The choice of Eq. 1.18 follows from several considerations:

1. It is linear in x and x', so that a single event in frame S corresponds to a single event in frame S', as it must.

2. It is simple, and a simple solution to a problem should always be explored first.

3. It has the possibility of reducing to Eq. 1. 11, which we know to be correct in ordinary mechanics. 

Because the equations of physics must have the same form in both S and S', we need only change the sign of c (in order to take into account the difference in the direction of relative motion) to write the corresponding equation for x in terms of x' and t':

1.19

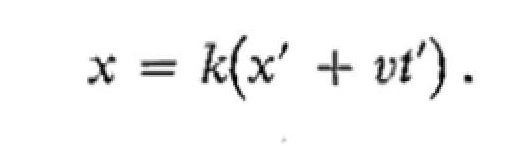
The factor k must be the same in both frames of reference since there is no difference between S and ,S' other than in the sign of v.

As in the case of the Galilean transformation, there is nothing to indicate that there might be differences between the corresponding coordinates y, y' and z, z' which are normal to the direction of v. Hence we again take 

1.20  1.21

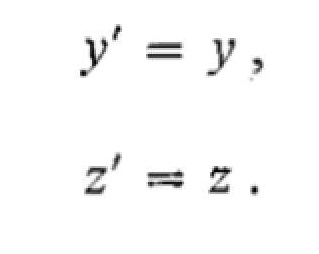
The time coordinates t and t' , however, are not equal. We can see this by substituting the value of x' given by Eq. 1.18 into Eq. 1.19. We obtain 

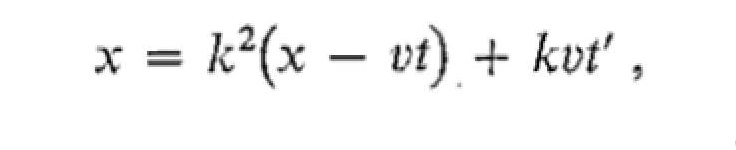
from which we find that

1.22 

Equations 1.18 and 1.20 to 1.22 constitute a coordinate transformation that satisfies the first postulate of special relativity. 

The second postulate of relativity enables us to evaluate k. At the instant t = 0, the origins of the two frames of reference S and S" are in the same place, according to our initial conditions, and t'=0 then also. Suppose that a flare is set off at the common origin of S and S' at t = t' = 0, and the observers in each system proceed to measure the speed with which the light from it spreads out. Both observers must find the same speed c (Fig. 1-7), which means that in the S frame

1.23

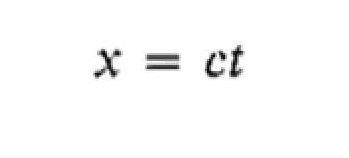
while in the S' frame

 1.24

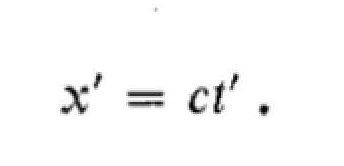
Substituting for x' and t' in Eq. 1.24 with the help of Eqs. 1.18 and 1.22, 

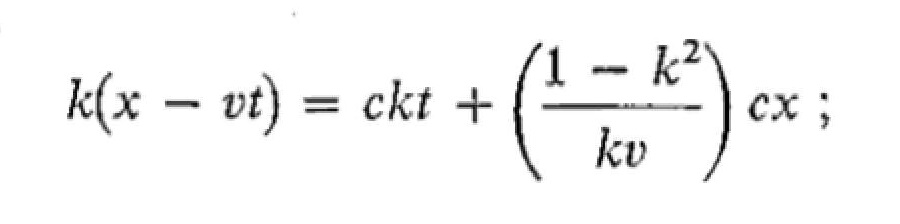
and solving for x, 

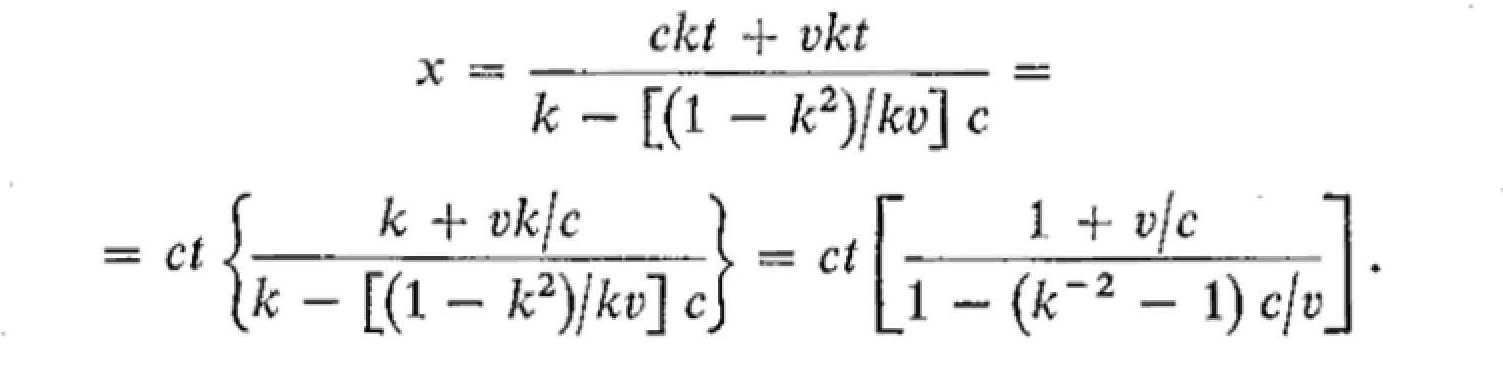
This expression for x will be the same as that given by Eq. 1.23, namely x = ct, provided that the quantity in the brackets equals 1. Therefore

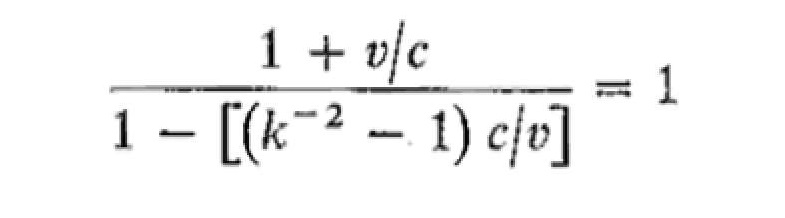
and

1.25

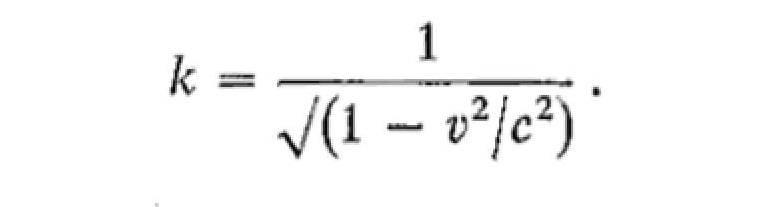
(until then it is a quote from the said book)

-

-

-

however, k is a function of v, so we should modify (all postulates are met) equation 1.19

x = k'(x' + vt')

where k' = k(-v)

then we would calculate

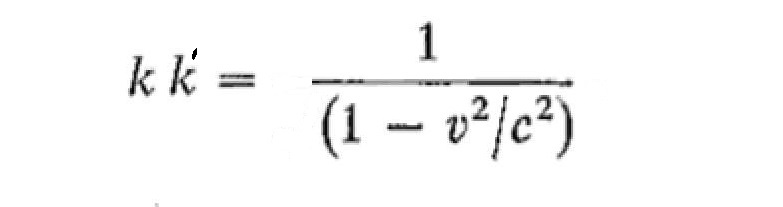
then these equations could also be the solution

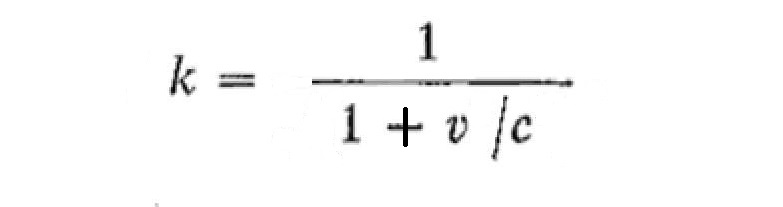
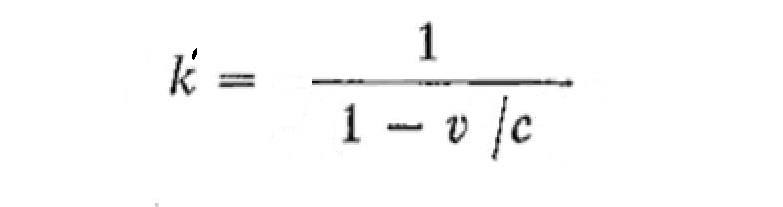
The Lorentz transformation therefore has other solutions than the standard calculation too